AEROFOIL THEORY

Every theory will contain some assumptions and some basic tools required.Here those basic tools will be discussed.

>>Primarily consider the surface of the aerofoil is with vortex completely and this is applicable for
only thin aerofoil.

>>FOr thin aerofoil to formulate flow characteristics over the aerofoil are obtained as follows:

 

     *On the surface of the aerofoil i.e upper and lower surfaces,simple vortex is assumed everywhere.

     *If aerofoil is viewed from for away distance it appears to fall on chord  or chamberline.

     *Hence is assumed that to analysing flow characteristics over aerofoil simple vortex on the chord
or chamberline.

BASIC TOOLS:

>> Consider a simple vortex at point "o" with strength  Г .

>> Imagie a straight line passing through origin "o".

      and the straight line is etended to the -∞ to +∞ .

 >>Infinite number of simple vortex on the straight line to be imagined.

>>Call the line as the straight vortex filament and strength of the vortex filament is  Г as the simple
vortex.

>>The straight vortex filament induces a velocity and imagine infinite number of straight vorte filaments.

>>The side by side vortex filaments also forms straight vortex sheet. 

>>The strength of each straight vortex filament is very small.

>>Consider the edge view of the vortex sheet we obtain a curve line in XZ-plane.

>>Since it is a continues portion of the sheet taking up the distance measured from a to b is S.

>>Consider a small distance ds. ४ is the strength of the vortex line sheet per unit length.

           strength of the vortex sheet of length   ds=४.ds

>>The strength of entire vortex sheet=Г.

                                  

>>Consider a point P in the element distance 'r'. r is the distance from the point p to the element vortex sheet.

>>The velocity induced at elemental vortex sheet will be as dv is the velocity induced by elemental vortex sheet.

                                                           dv=(-४.ds)/2πr.

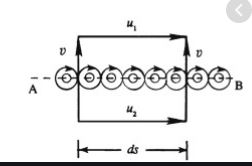
>>Consider elemental size of vortex sheet of ds.Length in a rectangle box.

>>Circulation around the rectangular box or closed path.

४=(u1-u2)

>>It states that local jump in tangential velocity across the vortex sheet equal to the local strength of the sheet with the given length.

KUTTA condition:

>>Actual airfoil trailing edge is having a finite angle.In theoritical aerofoil the upper surface and lower surface will form a point.

>>Velocity along the upper surface and lower surface is v1 and v2. v1 is parallel to upper surface at point a. v2 is parallel to lower surface at point a.

>>For the finite angle trailing edge it appears that at point a. we will have two different velocities in two different direction.

>>It is not physically possible if v1 and v2 are finite.only possible when v1=v2=0.

>>For the finite angle trailing edge point a trailing edge is a stagnation point.

>>For theoritical aerofoil v1=v2=0.since direction is same.

summary:

>>For a given aerofoil at a give angle of attack the value of  ४  around aerofoil is such that the flow leaves the trailing edge smoothly.

>>If the trailing edge is a finite angle,trailing edge is the stagnation point.

>>If the trailing edge is the cuspid then the velocities leaving the top and bottom surface are finite and equal in magnitude and direction.

POTENTIAL FLOW THEORY

INTRODUCTION:

This particular flow is a ideal flow which is not a real flow.This particular flow may not be there in physically possible flows due to viscosity.we consider potential flow as the non-viscous flow i.e neglecting viscosity.This potential flow will help us to understand the lift force on an object.But doesn't talk about the drag force.

continuity equation:

       velocity vector⇒ v=uî+vĴ

       then,

              ටu/ ටx   +   ටv/ ටy  = 0

             This is the continuity equation.

*The velocity vectors which satisfies the above equation such flow fields are physically possible flow  fields.That particular flow field will have a stream function (ψ) or else no streamm function.

Irrotationality:

   Rotational means rotating itself on its own axis.not rotating about a common axis.

              ටv/ ටx   -  ටu/ ටy  = 0

            This is irrotationality condition.

 DERIVATION FOR POTENTIAL FLOW EQUATIONS:

>>stream line is a mathematical line which flow velocity is tangential.

eq of stream line:

         udy -vdx =0

     

    u= ටψ/ටy      v=  - ටψ/ටx

   tanθ=dy/dx   =v/u.

eq of stream line:

>> udy -vdx =0

>>(ටψ/ටy)dy  -  (- ටψ/ටx)dx =0

>> (ටψ/ටx)dx + (ටψ/ටy)dy =0

      This is the total derivative of  ψ.

>>d ψ=0

      integrating on both sides

>> ψ=const.

*This says that along any stram line, stream function is constant.

*Another point is no two stream lines have the same stream function  ψ.

From  irrotationality condition:

>>  ටv/ ටx   -  ටu/ ටy  = 0

>>ට(ටФ/ටy)/ ටx   -  ට(ටФ/ටx)/ ටy  = 0

*If a flow field is possible and irrotational it can have only  ψ.
*If the flow field is not possible and irrotational it can have Ф.
*suppose the flow field is possible,irrotational such flow field can be represented by ψ and Ф.

equations of potential flow:

If any flow have ψ and Ф.Then,it is called potential flow and it satisfies the below equations

and

   Фxx +Фyy =0.